৮ম শ্রেণি | গনিত | অধ্যায়- ০৭ | বৃত্তের খুঁটিনাটি | PDF: অষ্টম শ্রেণির প্রাথমিক গনিত বিষয়টির ৭ম অধ্যায়টি হতে বেশ কিছু গুরুত্বপূর্ণ বৃত্তের খুঁটিনাটি সম্পর্কিত সকল প্রশ্ন উত্তর গুলো আমাদের এই পোস্টে আলোচনা করা হয়েছে। অতএব সম্পূর্ণ পোস্টটি মনযোগ সহকারে পড়ুন।
বৃত্তের খুঁটিনাটি
১। O কেন্দ্রবিশিষ্ট বৃত্তে জ্যা PQ = x cm এবং OR⊥PQ।
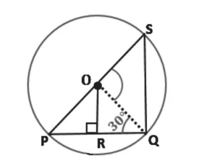
ক) ∠QOS এর পরিমাণ কত?
সমাধানঃ
ΔPOQ-এ,
PO = OQ [একই বৃত্তের ব্যাসার্ধ বলে]
∵∠QPO = ∠PQO = 30°[সমদ্বিবাহু ত্রিভুজের বাহুদ্বয়ের বিপরীত কোণদ্বয় সমান]
এখন,
∠QPO + ∠PQO + ∠POQ = 180°[ত্রিভুজের তিন কোণের সমষ্টি 180°]
বা, 30° + 30° + ∠POQ = 180°
বা, ∠POQ = 180° – 30° – 30°
বা, ∠POQ = 120° ……..(i)
আবার,
∠POS = 180°[∵ 1 সরলকোণ = 180°]
বা, ∠QOS + ∠POQ = 180°
বা, ∠QOS = 180° – ∠POQ
বা, ∠QOS = 180° – 120°[(i) নং হতে মান বসিয়ে]
∴∠QOS = 60°
খ) OR = (x/2 – 2) cm হলে, x এর মান নির্ণয় করো।
সমাধানঃ
দেওয়া আছে,OR = (x/2 – 2) cm;
PQ = x cm;
এখন,
ΔPOR ও ΔQOR -এ,
OR সাধারণ বাহু;
PO = QO [∵ একই বৃত্তের ব্যাসার্ধ]
∠ORP = ∠ORQ = 90°[∵ OR⊥PQ]
∵ΔPOR ≅ΔQOR
∵ PR = QR
∴ PR = ½PQ = ½x ………(i)
আবার,
ΔPOR-এ,
∠ORP = 90°[∵ OR⊥PQ]
∠RPO = 30°[∵PQ=OR]
∵∠POR = 180°-90°-30° = 60°
∵∠POR = 2∠RPO
∴ PR = 2OR = 2(x/2 – 2) ………(ii)
এখন, (i) ও (ii) হতে পাই,
½x = 2(x/2 – 2)
বা, ½x = x – 4
বা, x = 2x – 8
বা, x – 2x = – 8
বা, -x = -8
∴x = 8
২। 10 cm ও 24 cm দৈর্ঘের PQ ও RS সমান্তরাল জ্যা দুইটি O কেন্দ্রীয় বৃত্তের কেন্দ্রের বিপরীত পাশে অবস্থিত। যদি PQ ও RS জ্যা দুইটির মধ্যবর্তী দূরত্ব 17 cm হলে, বৃত্তের ব্যাসার্ধ নির্ণয় করো।
সমাধানঃ
মনে করি, O কেন্দ্রবিশিষ্ট PQSR বৃত্তে PQ ও RS দুইটি সমান্তরাল জ্যা যারা O এর দুই বিপরীত পাশে অবস্থিত এবং PQ = 10 cm ও RS = 24 cm. এবং PQ ও RS এর মধ্যবর্তী দূরত্ব 17 cm. বৃত্তের ব্যাসার্ধ নির্ণয় করতে হবে।
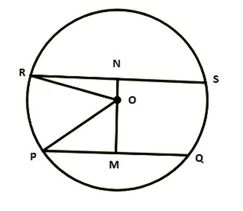
অঙ্কনঃ
O,R; O,P যোগ করি এবং O থেকে PQ এর উপর OM লম্ব এবং RS এর উপর ON লম্ব আঁকি।
বৃত্তের ব্যাসার্ধ নির্ণয়ঃ
PQ = 10 cm
∵ PM = 10/2 cm = 5 cm [বৃত্তের কেন্দ্র থেকে জ্যা এর উপর অঙ্কিত লম্ব জ্যা কে সমদ্বিখন্ডিত করে]
তাহলে, ΔOPM-এ,
OP2 = PM2 + OM2
∴ OP2 = 52 + OM2………(i)
আবার,
RS = 24 cm
∵ RN = 24/2 cm = 12 cm;
ΔNRO-এ,
RO2 = RN2 + ON2
∴OP2 =122 +(MN-OM)2…(ii) [∵RO=OP=বৃত্তের ব্যাসার্ধ]
এখন,
(i) ও (ii) হতে পাই,
52 + OM2 = 122 + (MN-OM)2
বা, 52 + OM2 = 122 + (17-OM)2
বা, 25 + OM2 = 144 + 172 – 2.17.OM+OM2
বা, 25 + OM2 = 144 + 289 – 34OM+OM2
বা, 25 + OM2 – 144 – 289 + 34OM-OM2 = 0
বা, 34OM -408 = 0
বা, 34OM = 408
∴ OM = 408/34 = 12 cm
এখন,
OM এর মান (i) নং এ বসিয়ে পাই,
OP2 = 52 + 122
বা, OP2 = 25 + 144
বা, OP2 = 169
বা, OP = 13
∴ বৃত্তের ব্যাসার্ধ = 13 cm.
৩। ধরো, তোমাদের একটি ত্রিভুজাকৃতি জমি আছে। জমিটির পরিসীমা 124 মিটার। ঐ জমির সবচেয়ে বেশি জায়গা জুড়ে সবজি চাষ করতে চাও। যদি সবজি চাষের জায়গার পরিধি 84 মিটার হয়, তবে জমিটির ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
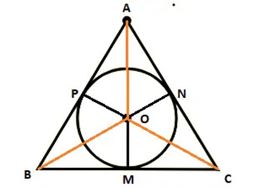
ধরি,
আমার একটি সবজি বাগান আছে যা নিন্মের চিত্রে ABC ত্রিভুজের ন্যায়। AB+BC+CA = 124 মিটার। ঐ জমির সবচেয়ে বেশি জায়গায় আমি সবজি করতে চাই, যার পরিধি 84 মিটার। এখন পরিধি বৃত্তক্ষেত্রের হয়ে থাকে অর্থাৎ বৃত্ত ক্ষেত্রটি এমন হবে যেন সেটি ত্রিভুজের সকল বাহুলে স্পর্শ করে ফলত সবজি চাষে বেশি জায়গা পাব। বৃত্তটি BC বাহুকে M; CA বাহুকে N; AB বাহুকে P বিন্দুতে স্পর্শ করে। বৃত্তের কেন্দ্র O; O,M; O,N; O,P যোগ করি।
এখন,
O কেন্দ্র বিশিষ্ট বৃত্তের ব্যাসার্ধ r হলে, প্রশ্নমতে,
2πr = 84
বা, r = 84/2π
বা, r = 13.368984 [∵π=3.1416]
চিত্রনুসারে, OM=ON=OP=r=13.368984
এখন, আমরা জানি,
বৃত্তের কোনো বিন্দুতে অঙ্কিত স্পর্শক, স্পর্শবিন্দুগামী ব্যাসার্ধের উপর লম্ব।
∵ OM⊥BC; ON⊥AC; OP⊥AB
তাহলে,
OM, OBC ত্রিভুজের উচ্চতা।
∵ΔOBC এর ক্ষেত্রফল
= ½×BC×OM
= ½×BC×13.368984
= 6.684492×BC
অনুরুপভাবে,
ΔAOC এর ক্ষেত্রফল = 6.684492×AC
ΔAOB এর ক্ষেত্রফল = 6.684492×AB
তাহলে,
ΔABC এর ক্ষেত্রফল
= ΔOBC এর ক্ষেত্রফল + ΔAOC এর ক্ষেত্রফল + ΔAOB এর ক্ষেত্রফল
=6.684492×BC+6.684492×ON+ 6.684492×OP
= 6.684492(BC+AC+AB)
= 6.684492×124
= 828.877008 বর্গ মিটার।
৪। চিত্রে O বৃত্তের কেন্দ্র এবং TA ও TC দুইটি স্পর্শক। ∠ATC = 60° হলে, x, y ও z এর মান নির্ণয় করো।
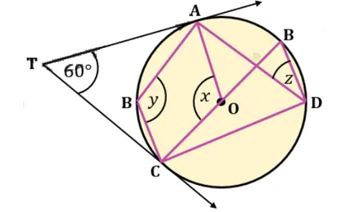
সমাধানঃ
চিত্রে O বৃত্তের কেন্দ্র এবং TA ও TC দুইটি স্পর্শক;
∵ ATCO-এ,
∠OAT = 90°; ∠OCT = 90°
∵∠OAT + ∠OCT + ∠ATC + ∠COA = 360°[চতুর্ভুজের চার কোণের সমষ্ট =360°]
বা, 90° + 90° + 60° + x = 360°
বা, 240° + x = 360°
বা, x = 360° – 240°
∴ x = 120°…….(i)
আবার,
x + ∠AOB = 180°[এক সরলকোণ]
∴∠AOB = 180°-120° = 60°
আবার,কেন্দ্রস্থ ∠AOC = 2×পরিধিস্থ ∠ADC [বৃত্তে কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ]
বা, 120° = 2×∠ADC [(i) নং থেকে মান বসিয়ে]
∴∠ADC = 120°/2 = 60° ……(ii)
আবার,
কেন্দ্রস্থ ∠COB = 2×পরিধিস্থ ∠CDB [বৃত্তে কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুণ]
বা, 180° = 2×∠CDB
বা, ∠CDB = 180°/2
বা, ∠CDB = 90°
বা, ∠ADC+∠ADB = 90°
বা, 60° + z = 90°[(ii) নং থেকে মান বসিয়ে]
∴ z = 90° -60° = 30° …….(iii)
আবার,360° – x
= 360° – 120°
= 240° যা x কোণ এর বিপরীত দিকের কেন্দ্রস্থ কোণ
= 2×পরিধিস্থ ∠ABC
= 2 × y
∵ 2y = 240°
∴ y = 240°/2 = 120° ……(iv)
অতএব, x = 120°; y = 120°; z = 30°

৫। একই আকারের (একই রকমের) কয়েকটি এক (১) টাকার কয়েন সংগ্রহ করো। কয়েনগুলোর যে কোনো একটিকে তোমার খাতার মাঝখানে রাখো। এবার এর চারপাশে পরস্পরকে স্পর্শ করে চিত্রের মতো কয়েনগুলো বসাও। অনেকটা ক্যারম বোর্ডে গুটি সাজানোর মতো।
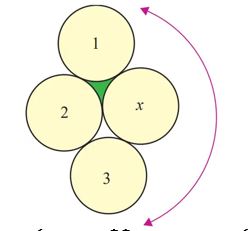
ক) উপরের শর্ত মেনে ‘x’ চিহ্নিত কয়েনকে স্পর্শ করে চারপাশে সর্বোচ্চ কটি কয়েন বসানো যাবে? চিত্রটি সম্পুর্ণ করে তা নির্ণয় করো।
সমাধানঃ
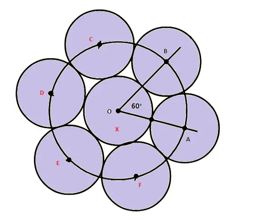
ধরি, x কয়েনের ব্যাসার্ধ = a
এখন, x কয়েনের কেন্দ্রে ∠BOA = 60° আঁকি।
O কে কেন্দ্র করে 2a এর সমান ব্যাসার্ধ নিয়ে একটি বৃত্ত ABCDEF আঁকি যা অঙ্কিত কোণের দুই বাহুকে যথাক্রমে A ও B তে ছেদ করে।
এখন, ABCDEF এর পরিধি = 2.Π.2a = 4Πa
এবং, AB চাপের দৈর্ঘ্য = 60/360×4Πa
∵ x কয়েনের চারপাশে সর্বোচ্চ কয়েন বসানো যাবে
= 4Πa ÷ 60/360×4Πa টি
= 6 টি।
উপরে চিত্রটি সম্পূর্ণ করা হলো এবং গণনা করে কয়েন সংখ্যা পেলাম 6 টি।
খ) চিত্রের ‘1’, ‘2’ ও ‘x’ চিহ্নিত বৃত্ত তিনটির কেন্দ্রগুলো যোগ করো। যে ত্রিভুজটি পেলে তার পরিসীমা 18 সেমি। চিত্রের সবুজ অংশের ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
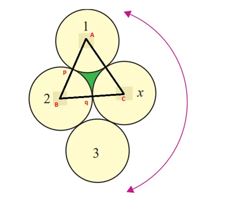
মনে করি,
কয়েন 1, 2 ও x এর কেন্দ্র যথাক্রমে A, B ও C. এবং প্রতিটি কয়েনের ব্যাসার্ধ = a.
তাহলে,
AB = a+a = 2a;
BC = a+a = 2a;
CA = a+a = 2a.
প্রশ্নমতে,
2a + 2a + 2a = 18
বা, 6a = 18
∴ a = 18/6 = 3 সেমি।
এবং, AB = 2.3 = 6; BC = 2.3 = 6; CA =2.3 = 6;
অর্থাৎ, AB=BC=CA = 6 সেমি।
∵ ABC এর ক্ষেত্রফল
= √3/4.(বাহুর দৈর্ঘ্য)2 বর্গ একক [সমবাহু ত্রিভুজের ক্ষেত্রফলের সূত্রমতে]
= √3/4.62 বর্গ সেমি
= 15.58845 বর্গ সেমি (প্রায়)
আবার,
সমবাহু ত্রিভুজের প্রতিটি কোণের পরিমাণ 60°.
এখন, 2 নং বৃত্তে PQ বৃত্তচাপ উৎপন্ন হয়েছে যার কেন্দ্রে কোণ 60°.
∵ বৃত্তকলাটির ক্ষেত্রফল
= 60/360×πr2 বর্গ একক
= 60/360×3.1416×32 বর্গ সেমি
= 4.7124 বর্গ সেমি।
অনুরুপভাবে 1, 2, x কয়েনে উৎপন্ন বৃত্তকলাত্রয়ের ক্ষেত্রফলের সমষ্টি
= 4.7124 বর্গ সেমি + 4.7124 বর্গ সেমি + 4.7124 বর্গ সেমি
= 14.1372 বর্গ সেমি
∵ বৃত্তকলা বাদে সবুজ অংশের ক্ষেত্রফল
= 15.58845 বর্গ সেমি – 14.1372 বর্গ সেমি
= 1.45125 বর্গ সেমি.
পড়ুনঃ
- English | Unseen Passage for Class 8 with Answers 31-35 | PDF
- English | Unseen Passage for Class 8 with Answers 36-40 | PDF
- English | Unseen Passage for Class 8 with Answers 41-45 | PDF
- English | Unseen Passage for Class 8 with Answers 46-50 | PDF
- Class 8 | English | Most Important Letter Writing 21-28 | PDF
গ) খাতায় চিত্রের যে কোনো একটি কয়েন ছাপ দিয়ে বৃত্ত বানাও। তারপর বৃত্তটির কেন্দ্র নির্ণয় করো।
সমাধানঃ
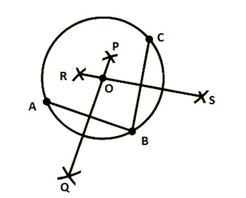
খাতায় x কয়েনের ছাপ দিয়ে ABC বৃত্তটি বানাই। এখন, ABC এর কেন্দ্র নির্ণয় করি।
কেন্দ্র নির্ণয়ঃ
(i) A, B; B, C যোগ করি।
(ii) A কে কেন্দ্র করে AB এর অর্ধেকের বেশি ব্যাসার্ধ নিয়ে AB এর উভয় পাশে দুইটি বৃত্তচাপ আঁকি। এবং B কে কেন্দ্র ঐ একই ব্যাসার্ধ নিয়ে AB এর উভয় পাশে দুইটি বৃত্তচাপ আঁকি। ফলত, দুই পাশের দুইটি বৃত্তচাপ পরস্পরকে P ও Q বিন্দুতে ছেদ করে। P, Q যোগ করি।
(iii) একইভাবে, B ও C কেন্দ্র করে বৃত্তচাপ আঁকি ফলত R ও S বিন্দু পাই। R, S যোগ করি।
(iv) এখন, PQ ও RS পরস্পরকে O বিন্দুতে ছেদ করে। তাহলে, O-ই উক্ত বৃত্তের কেন্দ্র।
ঘ) যে কোনো একটি কয়েনের ব্যাসার্ধের গুণিতক ব্যাসার্ধবিশিষ্ট দুইটি বৃত্ত আঁকো। বৃত্ত দুইটি পরস্পরকে বহিঃস্পর্শ করলে প্রমাণ করো যে, বৃত্ত দুইটির কেন্দ্রদ্বয়ের দূরত্ব তাদের সাধারণ ব্যাসার্ধের দ্বিগুণ।
সমাধানঃ
এই গাণিতিক সমস্যায় বৃত্তের সাধারণ ব্যাসার্ধ বিষয়টি আমাদের বোধগম্য হয় নি; আরও সময় নিয়ে আমরা এই সমস্যা নিয়ে ভাবব। তোমরাও আমাদেরকে তোমাদের মতামত জানিও।
উক্ত বিষয় সম্পর্কে কিছু জানার থাকলে কমেন্ট করতে পারেন।
আমাদের সাথে ইউটিউব চ্যানেলে যুক্ত হতে এখানে ক্লিক করুন এবং আমাদের সাথে ফেইজবুক পেইজে যুক্ত হতে এখানে ক্লিক করুন। গুরুত্বপূর্ণ আপডেট ও তথ্য পেতে আমাদের ওয়েবসাইটে ভিজিট করুন।


















