৯ম শ্রেণি | গনিত | অধ্যায় ৭ | কৌণিক দূরত্ব পরিমাপে ত্রিকোণমিতি: নবম ও দশম শ্রেণির প্রাথমিক গনিত বিষয়টির ৭ম অধ্যায়টি হতে বেশ কিছু গুরুত্বপূর্ণ কৌণিক দূরত্ব পরিমাপে ত্রিকোণমিতি সম্পর্কিত সকল সমাধান গুলো আমাদের এই পোস্টে আলোচনা করা হয়েছে। অতএব সম্পূর্ণ পোস্টটি মনযোগ সহকারে পড়ুন।
কৌণিক দূরত্ব পরিমাপে ত্রিকোণমিতি
1. 5° তে কত সেকেন্ড নির্ণয় করো।
সমাধান: আমরা জানি, 1° = 3600”
∵ 5° = (5×3600)” = 18000”
অর্থাৎ, 5° তে 18000 সেকেন্ড।
2. জ্যামিতিক রুলার এবং চাঁদা ব্যবহার করে 30°, 360°, 380°, -20° এবং –420° কোণ আঁক।
সমাধান:
30° অঙ্কনঃ
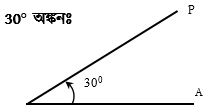
i) যেকোনো বিন্দু o নেই এবং জ্যামিতিক রুলার স্থাপন করে OA রশ্মি আঁকি।
ii) এবার চাঁদার কেন্দ্রকে O বিন্দুতে ও ডান পাশের প্রান্তভাগকে OA বরাবর মিলিয়ে স্থাপন করি যেন চাঁদার অর্ধবৃত্তাকার অংশ উপরের দিকে থাকে।
iii) এবার OA রশ্মি হতে ঘড়ির কাটার বিপরীত দিকে চাঁদা হতে 30 লেখা বরাবর পেন্সিল দিয়ে একটি বিন্দু P চিহ্নিত করি।
iv) O,P যোগ করে OP রশ্মি আঁকি; তাহলে ∠AOP = 30° অঙ্কিত হলো।
360° অঙ্কনঃ
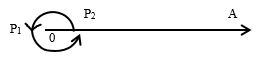
i) যেকোনো বিন্দু o নেই এবং জ্যামিতিক রুলার স্থাপন করে OA রশ্মি আঁকি।
ii) এবার চাঁদার কেন্দ্রকে O বিন্দুতে ও ডান পাশের প্রান্তভাগকে OA বরাবর মিলিয়ে স্থাপন করি যেন চাঁদার অর্ধবৃত্তাকার অংশ উপরের দিকে থাকে।
iii) এবার OA রশ্মি হতে ঘড়ির কাটার বিপরীত দিকে চাঁদার বামপাশে লেখা 180 বরাবর পেন্সিল দিয়ে একটি বিন্দু P1 চিহ্নিত করি। আবার, চাঁদার কেন্দ্রকে O বিন্দুতে ও ডান পাশের প্রান্তভাগকে OA বরাবর মিলিয়ে স্থাপন করি যেন চাঁদার অর্ধবৃত্তাকার অংশ নিচের দিকে থাকে। এবং চাঁদার ডানপাশে লেখা 180 বরাবর আরেকটি বিন্দু P2 চিহ্নিত করি।
iv) তাহলে, P2 বিন্দু OA এর সাথে সমাপতিত হয় ফলত OA রশ্মি বরাবর আমাদের 360° অঙ্কিত হলো।
380° অঙ্কনঃ
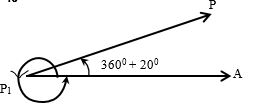
এখানে, 380° = 360° + 20°
অর্থাৎ, আমাদের 20° কোণ অঙ্কনই যথেষ্ট হবে কারণ 360° কোণ OA বরাবর অবস্থান করে।
i) যেকোনো বিন্দু o নেই এবং জ্যামিতিক রুলার স্থাপন করে OA রশ্মি আঁকি।
ii) এবার চাঁদার কেন্দ্রকে O বিন্দুতে ও ডান পাশের প্রান্তভাগকে OA বরাবর মিলিয়ে স্থাপন করি যেন চাঁদার অর্ধবৃত্তাকার অংশ উপরের দিকে থাকে।
iii) এবার OA রশ্মি হতে ঘড়ির কাটার বিপরীত দিকে চাঁদা হতে 20 লেখা বরাবর পেন্সিল দিয়ে একটি বিন্দু P চিহ্নিত করি।
iv) O,P যোগ করে OP রশ্মি আঁকি; তাহলে 360° + 20° = 380° অঙ্কিত হলো যা চিত্রে দেখানো হয়েছে।
-20° অঙ্কনঃ
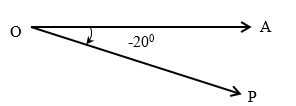
i) যেকোনো বিন্দু o নেই এবং জ্যামিতিক রুলার স্থাপন করে OA রশ্মি আঁকি।
ii) এবার চাঁদার কেন্দ্রকে O বিন্দুতে ও ডান পাশের প্রান্তভাগকে OA বরাবর মিলিয়ে স্থাপন করি যেন চাঁদার অর্ধবৃত্তাকার অংশ নিচের দিকে থাকে।
iii) এবার OA রশ্মি হতে ঘড়ির কাটার দিকে চাঁদা হতে 20 লেখা বরাবর পেন্সিল দিয়ে একটি বিন্দু P চিহ্নিত করি।
iv) O,Pযোগ করে OP রশ্মি আঁকি; তাহলে ∠AOP =-20° অঙ্কিত হলো।
-420° অঙ্কনঃ
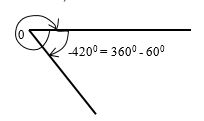
এখানে, -420° = -360° – 60°
অর্থাৎ, আমাদের -60° কোণ অঙ্কনই যথেষ্ট হবে কারণ -360° কোণ OA বরাবর অবস্থান করে।
i) যেকোনো বিন্দু o নেই এবং জ্যামিতিক রুলার স্থাপন করে OA রশ্মি আঁকি।
ii) এবার চাঁদার কেন্দ্রকে O বিন্দুতে ও ডান পাশের প্রান্তভাগকে OA বরাবর মিলিয়ে স্থাপন করি যেন চাঁদার অর্ধবৃত্তাকার অংশ নিচের দিকে থাকে।
iii) এবার OA রশ্মি হতে ঘড়ির কাটার দিকে চাঁদা হতে 60 লেখা বরাবর পেন্সিল দিয়ে একটি বিন্দু P চিহ্নিত করি।
iv) O,P যোগ করে OP রশ্মি আঁকি; তাহলে -360° – 60° = -420° অঙ্কিত হলো যা চিত্রে দেখানো হয়েছে।
3. রুলার এবং চাঁদা ব্যবহার করে 60°, 90°, 180°, 200°, 280°, 750°, –45°, –400° কোণগুলো আদর্শ অবস্থানে আঁকো। এগুলো কোয়াড্রেন্ট নাকি কোয়াড্রেন্টাল কোণ তা নির্ণয় করো। কোণগুলো কোন চতুর্ভাগে আছে তা উল্লেখ করো।
সমাধান: রুলার এবং চাঁদা ব্যবহার করে 60°, 90°, 180°, 200°, 280°, 750°, –45°, –400° কোণগুলো আদর্শ অবস্থানে আঁকা হলো যা নিন্মের চিত্রে অঙ্কিত।
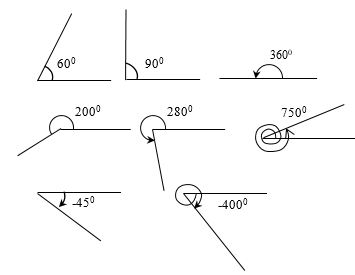
এখন কোণগুলোর অবস্থান বিবেচনা করে পাই,
60°, 200°, 280°, 750°, –45°, –400° কোণগুলো চারটি চতুর্ভাগের যেকোণ একটির ভিতরে অবস্থান করছে অর্থাৎ এরা কোয়াড্রেন্ট কোণ (quadrant angle)।
আবার, 90°, 180° কোণদুটি অক্ষের উপর অবস্থান করছে অর্থাৎ এরা কোয়াড্রেন্টাল কোণ (quadrantal angle)।
4. মান নির্ণয় করো :
cos135°, cot120°, tan390°, sin(–30°), sec300°, cos(–570°)
সমাধান:
cos135°
= cos(180°-45°)
= -cos45°
= – 1/√2 [∵cos45°= 1/√2]
cot120°
= cot(180°-60°)
= -cot60°
= – 1/√3 [∵cot60°= 1/√3]
tan390°
= tan(360°+30°)
= tan30°
= 1/√3 [∵tan30°= 1/√3]
sin(–30°)
= -sin30°
= – 1/√2 [∵sin30°= 1/√2]
sec300°
= sec(360°-60°)
= sec60°
= 2 [∵sec60°=2]
csc(–570°)
= csc570°
= csc(540°+30°)
= csc30°
= 2
5. আদর্শ অবস্থানে A(2, 3), B(–3, 1), C(–4, –4), D(1, –2), E(–2,0) বিন্দুগুলো দ্বারা উৎপন্ন কোণের ত্রিকোণমিতিক অনুপাত নির্ণয় করো।
সমাধান: A(2, 3)
এখানে, x=2, y=3 এবং r = √(22+32) = √13
সুতরাং ত্রিকোণমিতিক অনুপাতগুলোঃ
sinθ = y/r = 3/√13
cosθ = x/r = 2/√13
tanθ = y/x = 3/2
cotθ = x/y = 2/3
secθ = r/x = √13/2
cscθ = r/y = √13/3
B(–3, 1)
এখানে, x=-3, y=1 এবং r = √{(-3)2+12} = √10
সুতরাং ত্রিকোণমিতিক অনুপাতগুলোঃ
sinθ = y/r = 1/√10
cosθ = x/r = (-3)/√10
tanθ = y/x = 1/(-3)
cotθ = x/y = (-3)/1= -3
secθ = r/x = √10/(-3)
cscθ = r/y = √10/1= √10
C(–4, –4)
এখানে, x=-4, y=4 এবং r = √{(-4)2+42)} = √32 = 4√2
সুতরাং ত্রিকোণমিতিক অনুপাতগুলোঃ
sinθ = y/r = 4/(4√2) = 1/√2
cosθ = x/r = (-4)/(4√2) = (-1)/√2
tanθ = y/x = 4/(-4) = -1
cotθ = x/y = (-4)/4 = -1
secθ = r/x = (4√2)/(-4) = -√2
cscθ = r/y = (4√2)/4 = √2
D(1, –2)
এখানে, x=1, y=-2 এবং r = √{12+(-2)2} = √5
সুতরাং ত্রিকোণমিতিক অনুপাতগুলোঃ
sinθ = y/r = (-2)/√5
cosθ = x/r = 1/√5
tanθ = y/x = (-2)/1 = -2
cotθ = x/y = 1/(-2) = -1/2
secθ = r/x = √5/1 = √5
cscθ = r/y = √5/2
E(–2,0)
এখানে, x=-2, y=0 এবং r = √{(-2)2+02} = 2
সুতরাং ত্রিকোণমিতিক অনুপাতগুলোঃ
sinθ = y/r = 0/2 = 0
cosθ = x/r = (-2)/2 = -1
tanθ = y/x = 0/(-2) = 0
cotθ = x/y = (-2)/0 = undefined
secθ = r/x = 2/(-2) = -1
cscθ = r/y = 2/0 = undefined
6. নিম্নোক্ত বিন্দুগুলোকে r এবং tanθ এর মাধ্যমে প্রকাশ করো।
a. A(3, –2)
সমাধান:
এখানে, x=3, y=-2
∵ r = √{32+(-2)2} = √13
এবং, tanθ = y/x = -2/3
∵ A(3, –2) = (√13, (-2)/3 ) [প্রকাশ করা হলো]
b. B(–2, –1)
সমাধান: এখানে, x=-2, y=-1
∵ r = √{(-2)2+(-1)2} = √5
এবং, tanθ = y/x = (-1)/(-2) = 1/2
∵ A(-2, –1) = (√5, 1/2) [প্রকাশ করা হলো]
c. C(–4, 0)
সমাধান: এখানে, x=-4, y=0
∵ r = √{(-4)2+02} = 4
এবং, tanθ = y/x = 0/(-4) = 0
∵ A(-4, 0) = (4, 0) [প্রকাশ করা হলো]

পড়ুনঃ
- আম আঁটির ভেঁপু গল্পের জ্ঞান ও অনুধাবনমূলক প্রশ্ন ও উত্তর (PDF)
- বাংলা ১ম: বই পড়া গল্পের জ্ঞান ও অনুধাবনমূলক প্রশ্ন ও উত্তর (PDF)
- (PDF) পল্লিসাহিত্য কবিতার জ্ঞান ও অনুধাবনমূলক প্রশ্ন ও উত্তর
- SSC-জ্ঞানমূলক ও অনুধাবনমূলক সব প্রশ্নের উত্তর | কপোতাক্ষ নদ
7. রেডিয়ানে প্রকাশ কর:
a. 75°30’
সমাধান: 75°30’
= 75° + (30/60)° [∵1° = 60’]
= 75° + (1/2)°
= {((75×2+1))/2}°
= (151/2)°
= (151/2 π)/180 রেডিয়ান [∵1° = π/180 রেডিয়ান] = 151π/360 রেডিয়ান
b. 45°44’43’’
সমাধান: 45°44’43”
= 45° + (44/60)° + (43/3600)° [∵1° = 60’ এবং 1° = 3600”]
= π/180 (45 + 44/60 + 43/3600) রেডিয়ান [∵1° = π/180 রেডিয়ান]
= π/180 × (45×3600+44×60+43)/3600 রেডিয়ান
= (π(45×3600+44×60+43))/(3600×1800) রেডিয়ান
= 164683π/648000
c. 60°30’15’’
সমাধান: 60°30’15’’
= 60° + (30/60)° + (15/3600)° [∵1° = 60’ এবং 1° = 3600”]
= 60° + (1/2)° + (1/240)°
= π/180 (60 + 1/2 + 1/240) রেডিয়ান [∵1° = π/180 রেডিয়ান]
= π/180 × (60×240+1×120+1)/240 রেডিয়ান
= (π(14400+120+1))/(240×180) রেডিয়ান
= 14521π/43200 রেডিয়ান
8. ডিগ্রীতে প্রকাশ কর:
a. 4π/25 রেডিয়ান
সমাধান: 4π/25 রেডিয়ান
= (4π/25×180/π)° [∵1= 〖180〗^0/π]
= (4π/25 × 180/π)° = 28.8°
b. 1.3177 রেডিয়ান
সমাধান: 1.3177 রেডিয়ান
= (1.3177 × 180/π)° [∵1 = 〖180〗^0/π]
= (1.3177 × 180/3.1416)° [∵π =3.1416]
= 75.4984° (প্রায়)
c. 0.9759 রেডিয়ান
সমাধান: 0.9759 রেডিয়ান
= (0.9759 × 180/π)° [∵1 = 〖180〗^0/π]
= (0.9759 × 180/3.1416)° [∵π =3.1416]
= 55.9148° (প্রায়)
9. পৃথিবীর ব্যাসার্ধ 6440 কিলোমিটার। যদি টেকনাফ ও তেঁতুলিয়ার অবস্থান পৃথিবীর কেন্দ্রে 10°6’3’’ কোণ উৎপন্ন করে, তবে টেকনাফ থেকে তেঁতুলিয়ার দূরত্ব কত?
সমাধান:
এখানে, পৃথিবীর ব্যাসার্ধ, r = 6440 কিমি।
টেকনাফ ও তেঁতুলিয়ার অবস্থান দ্বারা পৃথিবীর কেন্দ্রে উৎপন্ন কোণ, θ = 10°6’3’’
= 10° + ( 6/60 )° + ( 3/3600 )°
= 10° + ( 1/10 )° + ( 1/1200 )°
= {((1200×10+120+1))/1200}°
= (12121/1200)°
= π/180 × 12121/1200 রেডিয়ান
= 12121π/216000 রেডিয়ান
সুতরাং, টেকনাফ ও তেঁতুলিয়ার দুরত্ব, s= rθ
= 6440 × 12121π/216000 = 1135.328 কিমি (প্রায়)
10. পৃথিবীর ব্যাসার্ধ 6440 কিলোমিটার। ধরো, পৃথিবীর উপরে দুইটি স্যাটেলাইট এমন অবস্থানে আছে যে তারা পৃথিবীর কেন্দ্রে 33’’ কোণ উৎপন্ন করে। স্যাটেলাইট দুইটির মধ্যবর্তী দূরত্ব কত?
সমাধানঃ
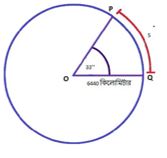
চিত্রে বৃত্তটিকে পৃথিবী ধরে নিয়ে সহজে আমরা এই সমস্যার সমাধান করতে পারি যেখানে,
OA = r = 6440 কিমি = পৃথিবীর ব্যাসার্ধ
∠POQ = θ = 33” = (33/3600)° = π/180 ×33/3600 রেডিয়ান
P ও Q হলো পৃথিবীর উপরে অবস্থিত দুইটি স্যাটেলাইট।
s = P ও Q এর দূরত্ব বের করতে হবে।
সুতরাং, স্যাটেলাইট দুইটির মধ্যবর্তী দূরত্ব, s
= rθ
= 6440 × π/180 × 33/3600 কি.মি.
= 1 কি.মি. (প্রায়)
উক্ত বিষয় সম্পর্কে কিছু জানার থাকলে কমেন্ট করতে পারেন।
আমাদের সাথে ইউটিউব চ্যানেলে যুক্ত হতে এখানে ক্লিক করুন এবং আমাদের সাথে ফেইজবুক পেইজে যুক্ত হতে এখানে ক্লিক করুন। গুরুত্বপূর্ণ আপডেট ও তথ্য পেতে আমাদের ওয়েবসাইটে ভিজিট করুন।


















