৯ম শ্রেণি | গনিত | অধ্যায় ১ম | প্রাত্যহিক জীবনে সেট | PDF: নবম ও দশম শ্রেণির প্রাথমিক গনিত বিষয়টির ১ম অধ্যায়টি হতে বেশ কিছু গুরুত্বপূর্ণ প্রাত্যহিক জীবনে সেট সম্পর্কিত সকল সমাধান গুলো আমাদের এই পোস্টে আলোচনা করা হয়েছে। অতএব সম্পূর্ণ পোস্টটি মনযোগ সহকারে পড়ুন।
প্রাত্যহিক জীবনে সেট
১। তালিকা পদ্ধতিতে প্রকাশ করো :
ক) A = {x ∈ N : –3 < x ≤ 5}
সমাধানঃ ক) A = {x ∈ N : –3 < x ≤ 5}
এখানে, N = {1, 2, 3, 4 … }
-3 থেকে বড় সংখ্যাগুলো হলোঃ -2,-1,0,1,2,3,4,5,6, …
5 এর সমান ও ছোট সংখ্যাগুলো হলোঃ
5,4,3,2,1,0,-1,-2,-3, …
অর্থাৎ, –3 < x ≤ 5 শর্ত পূরণ করা সংখ্যাগুলো হলোঃ
-2,-1,0,1,2,3,4,5
তাহলে, A={-2,-1,0,1,2,3,4,5} [Ans.]
খ) B = {x ∈ Z : x মৌলিক সংখ্যা এবং x2 ≤ 50}
সমাধানঃ এখানে,
Z = পূর্ণ সংখ্যার সেট = { … , -3,-2,-1,0,1,2,3,4,5… }
মৌলিক সংখ্যাগুলো হলোঃ 2,3,5,7,11,13 …
এখন,
22 = 4 ≤ 50
32 = 9 ≤ 50
52 = 25 ≤ 50
72 = 49 ≤ 50
112 = 121 > 50
অতএব, B = {2,3,5,7} [Ans.]
গ) C = {x ∈ Z : x4 < 264}
সমাধানঃ এখানে,
Z = পূর্ণ সংখ্যার সেট = {….-3,-2,-1,0,1,2,3,4,5 …}
এখন,
| 04 = 0 < 264
14 = 1 < 264 24 = 16 < 264 34 = 81 < 264 44 = 256 < 264 54 = 625 > 264 |
(-1)4 = 1 < 264 (-2)4 = 16 < 264 (-3)4 = 81 < 264 (-4)4 = 256 < 264 (-5)4 = 625 > 264 |
অতএব, C = {-4,-3,-2,-1,0,1,2,3,4} [Ans.]
২। সেট গঠন পদ্ধতিতে প্রকাশ করো :
ক) A = {1, 3, 5, … ,101}
সমাধানঃ এখানে, A = {1, 3, 5, … , 101}
অর্থাৎ, x এর মান সর্বনিন্ম 1 এবং সর্বোচ্চ 101 এবং এখানে সকল সংখ্যা স্বাভাবিক বিজোড় সংখ্যা।
∴ A= {x∈N:x,স্বাভাবিক বিজোড় সংখ্যা যেখানে, 1≤x≤101}[Ans.]
খ) B = {4, 9, 16, 25, 36, 49, 64, 81, 100}
সমাধানঃ এখানে,
B = {4, 9, 16, 25, 36, 49, 64, 81, 100}
= {22,32,42,52,62,72,82,92,102}
তাহলে, x এর মানগুলো স্বাভাবিক সংখ্যার বর্গ এবং এই সকল স্বাভাবিক সংখ্যার সর্বনিন্ম মান 2 এবং সর্বোচ্চ মান 10.
∴ A={x ∈ N: x, স্বাভাবিক সংখ্যার বর্গ যেখানে, 2≤N≤10} [Ans.]
৩। যদি A = {1, 2, 3, 4, 5}, B = {0, 1, 3, 5, 6} এবং C = {1, 5, 6} হয়, তবে নিচের সেটগুলো নির্ণয় করো।
ক) A ∪ B
সমাধানঃ দেওয়া আছে,
A = {1, 2, 3, 4, 5}, B = {0, 1, 3, 5, 6}
∴ A ∪ B = {1,2,3,4,5} ∪ {0,1,3,5,6}
= {0,1,2,3,4,5,6} [Ans.]
খ) A ∩ C
সমাধানঃ দেওয়া আছে,
A = {1, 2, 3, 4, 5}, C = {1, 5, 6}
∴ A ∩ C = {1,2,3,4,5} ∩ {1, 5, 6}
= {1,5} [Ans.]
গ) B╲C
সমাধানঃ দেওয়া আছে,
B = {0, 1, 3, 5, 6}, C = {1, 5, 6}
∴ B╲C = {0, 1, 3, 5, 6} ╲ {1, 5, 6}
= {0,3,} [Ans.]
ঘ) A ∪ (B ∩ C)
সমাধানঃ দেওয়া আছে,
A = {1, 2, 3, 4, 5}, B = {0, 1, 3, 5, 6} এবং
C = {1, 5, 6}
∴ B ∩ C
= {0, 1, 3, 5, 6} ∩ {1, 5, 6}
= {1, 5, 6}
∴ A ∪ (B ∩ C)
= {1, 2, 3, 4, 5} ∪ {1,5,6}
= {1, 2, 3, 4, 5, 6} [Ans.]
ঙ) A ∩ (B ∪ C)
সমাধানঃ দেওয়া আছে,
A = {1, 2, 3, 4, 5}, B = {0, 1, 3, 5, 6} এবং
C = {1, 5, 6}
∴ B ∪ C
= {0, 1, 3, 5, 6} ∪ {1, 5, 6}
= {0, 1, 3, 5, 6}
∴ A ∩ (B ∪ C)
= {1, 2, 3, 4, 5} ∪ {0,1,3,5,6}
= {1, 3, 5} [Ans.]
৪। যদি U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 3, 5, 7}, B ={0, 2, 4, 6} এবং C = {3, 4, 5, 6, 7} হয়, তবে নিম্নলিখিত ক্ষেত্রে সত্যতা যাচাই করো :
ক) (A ∪ B)c = Ac ∩ Bc
সমাধানঃ দেওয়া আছে,
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A ={1,3,5, 7}, B ={0, 2, 4, 6} এবং C = {3, 4, 5, 6, 7}
এখন,
বামপক্ষ
= (A ∪ B)c
= U – (A ∪ B)
= U – ({1, 3, 5, 7} ∪ {0, 2, 4, 6})
= U – {0,1,2,3,4,5,6,7}
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – {0,1,2,3,4,5,6,7}
= {8,9}
ডানপক্ষ
= Ac ∩ Bc
= (U –A) ∩ (U-B)
= [{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}]– {1, 3, 5, 7} ∩
[{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}-{0, 2, 4, 6}]
= {0,2,4,6,8,9} ∩ {1,3,5,7,8,9} = {8,9}
∴ বামপক্ষ = ডানপক্ষ [সত্যতা যাচাই করা হলো]
খ) (B ∩ C)c = Bc ∪ Cc
সমাধানঃ দেওয়া আছে,
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
A = {1, 3, 5, 7},
B = {0, 2, 4, 6} এবং
C = {3, 4, 5, 6, 7}
বামপক্ষ
= (B ∩ C)c
= U – (B ∩ C)
= U – [{0, 2, 4, 6} ∩ {3, 4, 5, 6, 7}]
= U – {4, 6}
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} – {4,6}
= {0, 1, 2, 3, 5, 7, 8, 9}
ডানপক্ষ
= Bc ∪ Cc
= (U-B) ∪ (U-C)
= [{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}-{0, 2, 4, 6}] ∪
[{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}-{3, 4, 5, 6, 7}]
= {1, 3, 5, 7, 8, 9} ∪ {0, 1, 2, 8, 9}
= {0, 1, 2, 3, 5, 7, 8, 9}
∴ বামপক্ষ = ডানপক্ষ [সত্যতা যাচাই করা হলো]
গ) (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
সমাধানঃ দেওয়া আছে,
A = {1, 3, 5, 7}, B = {0, 2, 4, 6} এবং
C = {3, 4, 5, 6, 7}
বামপক্ষ
= (A ∪ B) ∩ C
= ({1, 3, 5, 7} ∪ {0, 2, 4, 6}) ∩ {3, 4, 5, 6, 7}
= {0, 1, 2, 3, 4, 5, 6, 7} ∩ {3, 4, 5, 6, 7}
= {3, 4, 5, 6, 7}
ডানপক্ষ
= (A ∩ C) ∪ (B ∩ C)
= [{1, 3, 5, 7} ∩ {3, 4, 5, 6,7}] ∪ [{0, 2, 4, 6}
∩ {3, 4, 5, 6, 7}]
= {3, 5, 7} ∪ {4, 6}
= {3, 4, 5, 6, 7}
∴ বামপক্ষ = ডানপক্ষ [সত্যতা যাচাই করা হলো]
ঘ) (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C)
সমাধানঃ দেওয়া আছে,
A = {1, 3, 5, 7}, B = {0, 2, 4, 6} এবং
C = {3, 4, 5, 6, 7}
বামপক্ষ
= (A ∩ B) ∪ C
= ({1, 3, 5, 7} ∩ {0, 2, 4, 6}) ∪ {3, 4, 5, 6, 7}
= ∅ ∪ {3, 4, 5, 6, 7}
= {3, 4, 5, 6, 7}
ডানপক্ষ
= (A ∪ C) ∩ (B ∪ C)
= [{1, 3, 5, 7} ∪ {3, 4, 5, 6, 7}] ∩ [{0, 2,4, 6}
∪ {3, 4, 5, 6, 7}]
= {1, 3, 4, 5, 6, 7} ∩ {0, 2, 3, 4, 5, 6, 7}
= {3, 4, 5, 6, 7}
∴ বামপক্ষ = ডানপক্ষ [সত্যতা যাচাই করা হলো]
৫। মান নির্ণয় করো:
ক) N ∩ 2N, খ) N ∩ A, গ) 2N ∩ P
যেখানে, N সকল স্বাভাবিক সংখ্যার সেট, 2N সকল ধনাত্মক জোড় সংখ্যার সেট, A সকল বিজোড় সংখ্যার সেট, P সকল মৌলিক সংখ্যার সেট।
সমাধানঃ প্রশ্নমতে,
N = {1, 2, 3, 4, 5, 6, … }
2N ={2, 4, 6, 8, 10 … }
A = { … -7, -5, -3, -1, 1, 3, 5, 7, … }
P = { … -3, -2, -1, 0, 1, 2, 3, … }
তাহলে,
ক) N ∩ 2N
= {1, 2, 3, 4, 5, 6, … } ∩ {2, 4, 6, 8, 10, … }
= {2, 4, 6, 8, 10, … } [Ans.]
খ) N ∩ A
= {1,2,3, 4, 5, 6 …} ∩ {…-7,-5,-3,-1,1,3,5,7…}
= {1, 3, 5, 7, … } [Ans.]
গ) 2N ∩ P
= {2, 4, 6, 8, 10…} ∩ {… -3,-2,-1,0,1,2,3……}
= {2, 4, 6, 8, 10…} [Ans.]
৬। ধরি U সকল ত্রিভুজের সেট হয় এবং A সকল সমকোণী ত্রিভুজের সেট। তাহলে সেট Ac বর্ণনা করো।
সমাধানঃ প্রশ্নমতে,
U = সকল ত্রিভুজের সেট
A = সকল সমকোণী ত্রিভুজের সেট
=সেইসকল ত্রিভুজের সেট যেসকল ত্রিভুজের একটি
কোণ সমকোণ
∴ Ac = সেইসকল ত্রিভুজের সেট যেসকল ত্রিভুজের একটি
কোণ সমকোণ নয়
= সকল সূক্ষ্মকোণী ও স্থূলকোণী ত্রিভুজের সেট।
৭। ভেন চিত্রের মাধ্যমে দেখাও যে, যে কোনো সেট A, B, C এর জন্য
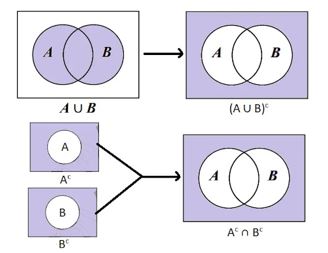
ক) (A ∪ B)c = Ac ∩ Bc
সমাধানঃ যে কোনো সেট A, B এর জন্য (A ∪ B)c ও Ac ∩ Bc এর ভেন চিত্র নিচে দেওয়া হলোঃ
অর্থাৎ, ভেনচিত্র হতে পাই, (A ∪ B)c = Ac ∩ Bc
খ) (B ∩ C)c = Bc ∪ Cc
সমাধানঃ যে কোনো সেট B, C এর জন্য (B ∩ C)c ও Bc ∪ Cc এর ভেন চিত্র নিচে দেওয়া হলোঃ
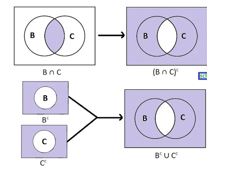
অর্থাৎ, ভেনচিত্র হতে পাই, (B ∩ C)c = Bc ∪ Cc
গ) (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
সমাধানঃ যে কোনো সেট A, B, C এর জন্য (A ∪ B) ∩ C ও (A ∩ C) ∪ (B ∩ C) এর ভেন চিত্র নিচে দেওয়া হলোঃ
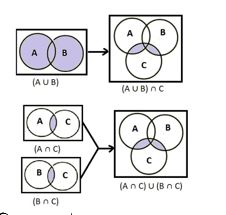
অর্থাৎ, ভেনচিত্র হতে পাই, (A∪B)∩C = (A∩C)∪(B∩C)
ঘ) (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C)
সমাধানঃ যে কোনো সেট A, B, C এর জন্য (A ∩ B) ∪ C ও (A ∪ C) ∩ (B ∪ C) এর ভেন চিত্র নিচে দেওয়া হলোঃ
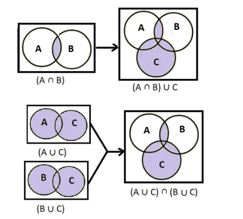
অর্থাৎ, ভেনচিত্র হতে পাই, (A∩B)∪C ও (A∪C)∩(B∪C)
৯ম শ্রেণি | গনিত | অধ্যায় ১ম | প্রাত্যহিক জীবনে সেট | PDF
৮। কোনো শ্রেণির 40 জন শিক্ষার্থীর মধ্যে 25 জন পাখি পছন্দ করে এবং 15 জন বিড়াল পছন্দ করে। পাখি ও বিড়াল দুটি প্রাণীই পছন্দ করে এরূপ শিক্ষার্থীর সংখ্যা 10 জন। কতজন শিক্ষার্থী পাখি ও বিড়াল কোনোটিই পছন্দ করে না তা ভেন চিত্রের সাহায্যে নির্ণয় করো।
সমাধানঃ
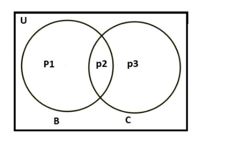
ভেন চিত্রে,
40 জন শিক্ষার্থীর সেট U আয়তক্ষেত্র দ্বারা নির্দেশ করি।
25 জন শিক্ষার্থী যারা পাখি পছন্দ করে তাদের সেট B বৃত্তক্ষেত্র দ্বারা নির্দেশ করি।
15 জন শিক্ষার্থী যারা বিড়াল পছন্দ করে তাদের সেট C বৃত্তক্ষেত্র দ্বারা নির্দেশ করি।
চিত্র অনুসারে, পাখি ও বিড়াল দুইটিই পছন্দ করে এমন শিক্ষার্থীর সংখ্যা p2 = 10 জন।
শুধু পাখি পছন্দ করে এমন শিক্ষার্থীর সংখ্যা p1 = B – p2 = 25 – 10 = 15 জন।
শুধু বিড়াল পছন্দ করে এমন শিক্ষার্থীর সংখ্যা p3 = C – p2 = 15 – 10 = 5 জন।
∴ শুধু পাখি+উভয়+শুধু বিড়াল পছন্দ করে p1+p2+p3 = 15+10+5 = 30 জন।
তাহলে,
পাখি বা বিড়াল এর কোনটিই পছন্দ করে না এমন শিক্ষার্থীর সংখ্যা = U– (p1+p2+p3)= 40– 30 = 10 জন।
∴ নির্নেয় উত্তরঃ 10 জন।
প্রাত্যহিক জীবনে সেট এর অনুশীলনীর সমাধান অর্থাৎ ৯ম শ্রেণির নতুন কারিকুলামের ১ম অধ্যায়ের অনুশীলনীর সকল প্রশ্নের পূর্ণাঙ্গ সমাধান প্রদান করা হয়েছে এখানে, সাথে চলার জন্য ধন্যবাদ। ১০০% সঠিক সমাধানে সচেষ্ট আমরা সর্বদা, চল এগিয়ে যাই।

৯। যদি P = {a, b}, Q = {0, 1, 2} এবং R = {0, 1, a} হয়, তবে নিচের রাশিগুলোর মান নির্ণয় করো।
ক) P × Q, P × P, Q × Q, Q × P এবং P × ∅
সমাধানঃ P × Q
= {a,b}×{0,1,2}
={(a,0), (a,1), (a,2), (b,0), (b,1), (b,2)}
P × P
={a,b}×{a,b}
={(a,a),(a,b),(b,a),(b,b)}
Q × Q
={0,1,2} ×{0,1,2}
={(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)}
Q × P
={0,1,2}×{a,b}
={(0,a),(a,b),(1,a),(1,b),(2,a),(2,b)}
এবং P × ∅ = ∅
খ) (P × Q) ∩ ( P × R)
সমাধানঃ (P × Q) ∩ ( P × R)
= ({a,b}×{0,1,2}) ∩ ({a,b}×{0,1,a})
= {(a,0), (a,1), (a,2), (b,0), (b,1), (b,2)}∩{(a,0),
(a,1), (a,a), (b,0),(b,1),(b,a)}
= {(a,0),(a,1),(b,0),(b,1)}
গ) P × (Q ∩ R)
সমাধানঃ P × (Q ∩ R)
= {a,b} × ({0,1,2} ∩ {0,1,a})
= {a,b} × {0,1}
= {(a,0), (a,1), (b,0), (b,1)}
ঘ) (P × Q) ∩ R
সমাধানঃ (P × Q) ∩ R
=({a,b}×{0,1,2}) ∩ {0,1,a}
= {(a,0),(a,1),(a,2),(b,0),(b,1),(b,2)} ∩ {0,1,a}
= ∅
ঙ) n(P × Q), n(Q × Q)
সমাধানঃ P × Q
= {a,b}×{0,1,2}
= {(a,0),(a,1),(a,2),(b,0),(b,1),(b,2)}
এখানে, P × Q এর উপাদান সংখ্যা 6 টি।
∴ n (P × Q) = 6
আবার, Q × Q
={0,1,2}×{0,1,2}
={(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)}
এখানে, Q × Q এর উপাদান সংখ্যা 9 টি।
∴ n (Q × Q) = 9
পড়ুনঃ
- আম আঁটির ভেঁপু গল্পের জ্ঞান ও অনুধাবনমূলক প্রশ্ন ও উত্তর (PDF)
- বাংলা ১ম: বই পড়া গল্পের জ্ঞান ও অনুধাবনমূলক প্রশ্ন ও উত্তর (PDF)
- (PDF) পল্লিসাহিত্য কবিতার জ্ঞান ও অনুধাবনমূলক প্রশ্ন ও উত্তর
- SSC-জ্ঞানমূলক ও অনুধাবনমূলক সব প্রশ্নের উত্তর | কপোতাক্ষ নদ
(চ) (গ) এবং (ঘ) এর সমতার বিষয়ে তোমার যুক্তি উপস্থাপন করো।
সমাধানঃ A ও B সেট যদি এমন হয় যে এদের উপাদানগুলো একই তবে A ও B একই সেট এবং তা A = B লিখে প্রকাশ করা হয়। যেমন A = {1, 2, 3, 4}, B = {1, 2, 2, 3, 4, 4, 4}। লক্ষ কর কোনো সেটে একই উপাদান বার বার থাকলেও সেটা একবার থাকার মতই বিবেচনা করা হচ্ছে। A = B হয় যদি ও কেবল যদি A⊆B এবং B⊆A হয়। সেট সমতা প্রমাণে এই তথ্য খুবই প্রয়োজনীয়।
অর্থ্যাৎ P× (Q∩R) =(P x Q) ∩(P x R) হয়।
সংজ্ঞানুসারে, P×(Q∩R)
={(x,y): x∈P, x∈Q এবং y∈R}
={(x,y): (x,y)∈P×Q এবং (x,y)∈P×R}
∴ P×(Q∩R)⊆(P×Q)∩(P×R)
আবার, (P×Q)∩(P×R)
={(x,y):(x,y)∈P×Q এবং (x,y)∈P×R}
={(x,y): x∈P, y∈Q এবং x∈P, y∈R}
∴ (P×Q)∩(P×R)⊆P×(Q∩R)
সুতরাং, P×(Q∩R)=(P×Q)∩(P×R)।
১০। P = {0, 1, 2, 3}, Q = {1, 3, 4} এবং R = P ∩ Q হলে,
(i) P × R এবং R × Q নির্ণয় করো।
সমাধানঃ দেওয়া আছে,
P = {0, 1, 2, 3}, Q = {1, 3, 4} এবং R = P ∩ Q
এখন, R
= P ∩ Q
= {0, 1, 2, 3} ∩ Q {1, 3, 4}
= {1,3}
∴ P × R
= {0, 1, 2, 3} × {1,3}
= {(0,1),(0,3),(1,1),(1,3),(2,1),(2,3),(3,1),(3,3)}
এবং R × Q
= {1,3} × {1, 3, 4}
= {(1,1),(1,3),(1,4),(3,1),(3,3),(3,4)}
(ii) n(P × R) এবং n(R × Q) এর মান বের করো।
সমাধানঃ (i) নং হতে পাই,
P × R এর গুণফলে উপাদান সংখ্যা 8টি
এবং R × Q এর গুণফলে উপাদান সংখ্যা 6টি
তাহলে, n(P × R) = 8 এবং n(R × Q) = 6
১১। যদি P × Q = {(0, a ), (1, c), (2, b)} হয়, তবে P এবং Q নির্ণয় করো।
সমাধানঃ দেওয়া আছে, P × Q = {(0, a ), (1, c), (2, b)}
এখানে,
P × Q এর উপাদানগুলোর ১ম রাশিগুলো হলোঃ 0,1,2 এবং ২য় রাশিগুলো হলোঃ a,c,b
তাহলে, P = {0,1,2} এবং Q = {a,c,b}
বিঃদ্রঃ এই হিসেবে P={0,1,2} এবং Q ={a,c,b} হতে হলে P×Q= {(0,a),(0,c),(0,b),(1,a),(1,c),(1,b),(2,a),(2,c),
(2,b)} হবে।
উক্ত বিষয় সম্পর্কে কিছু জানার থাকলে কমেন্ট করতে পারেন।
আমাদের সাথে ইউটিউব চ্যানেলে যুক্ত হতে এখানে ক্লিক করুন এবং আমাদের সাথে ফেইজবুক পেইজে যুক্ত হতে এখানে ক্লিক করুন। গুরুত্বপূর্ণ আপডেট ও তথ্য পেতে আমাদের ওয়েবসাইটে ভিজিট করুন।


















