৮ম শ্রেণি | গনিত | পরিমাপে প্রতিসমতার প্রয়োগ | PDF: অষ্টম শ্রেণির প্রাথমিক গনিত বিষয়টির ৮ম অধ্যায়টি হতে বেশ কিছু গুরুত্বপূর্ণ পরিমাপে প্রতিসমতার প্রয়োগ সম্পর্কিত সকল প্রশ্ন উত্তর গুলো আমাদের এই পোস্টে আলোচনা করা হয়েছে। অতএব সম্পূর্ণ পোস্টটি মনযোগ সহকারে পড়ুন।
পরিমাপে প্রতিসমতার প্রয়োগ
১. নিচের চিত্রগুলোর ঘূর্ণন কোণ এবং ঘূর্ণন প্রতিসমতার মাত্রা নির্ণয় করো।
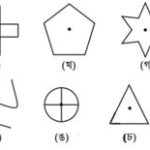
সমাধানঃ
(ক)
এখানে, 360°÷ 4 = 90° [যেহেতু, চিত্রে সদৃশ অংশ 4টি]
∵ ঘূর্ণন-কোণ = 90°এবং ঘূর্ণন-প্রতিসমতার মাত্রা = 4
(খ)
এখানে, 360°÷ 5 = 72° [যেহেতু, চিত্রে সদৃশ অংশ 5টি]
∵ ঘূর্ণন-কোণ = 72°এবং ঘূর্ণন-প্রতিসমতার-মাত্রা = 5
(গ)
এখানে, 360°÷ 6 = 60° [যেহেতু, চিত্রে সদৃশ অংশ 6টি]
∵ ঘূর্ণন-কোণ = 60°এবং ঘূর্ণন-প্রতিসমতার-মাত্রা = 6
(ঘ)
এখানে, 360°÷ 3 = 120° [যেহেতু, চিত্রে সদৃশ অংশ 3টি]
∵ ঘূর্ণন-কোণ = 120°এবং ঘূর্ণন-প্রতিসমতার-মাত্রা = 3
(ঙ)
এখানে, 360°÷ 4 = 90° [যেহেতু, চিত্রে সদৃশ অংশ 4টি]
∵ ঘূর্ণন কোণ = 90°এবং ঘূর্ণন প্রতিসমতার মাত্রা = 4
(চ)
এখানে, 360°÷ 3 = 120° [যেহেতু, চিত্রে সদৃশ অংশ 3টি]
∵ ঘূর্ণন কোণ = 120°এবং ঘূর্ণন প্রতিসমতার-মাত্রা = 3

২. (ক) এক মাত্রার ঘূর্ণন প্রতিসমতা বলতে কী বোঝ? একমাত্রার ঘূর্ণন প্রতিসমতার ঘূর্ণন কোণ কত? [পরিমাপে প্রতিসমতার প্রয়োগ অধ্যায়ের ২ নং এর ক প্রশ্ন এটি, উপরে নিয়ে সকল প্রশ্ন দেখ। ]
সমাধানঃ
কোণ বস্তু-ঘূর্ণন-প্রতিসমতার মাত্রা 1 হলে, তাকে এক মাত্রার ঘূর্ণন প্রতিসমতা বলে।
এবং, একমাত্রার ঘূর্ণন প্রতিসমতার-ঘূর্ণন কোণ= 360°÷1= 360°.
(খ) প্রতিসাম্য কোণ 20 ডিগ্রি হতে পারে কি? কারণ উল্লখ করো।
সমাধানঃ
360° ÷ 20° = 18;
অর্থাৎ, কোণ বস্তুর-প্রতিসাম্য-কোণ 20° হলে, এর প্রতিসমতার-
মাত্রা 18 হতে হবে।
∵ প্রতিসাম্য কোণ 20 ডিগ্রি হতে পারে।
পড়ুনঃ
- English | Unseen Passage for Class 8 with Answers 31-35 | PDF
- English | Unseen Passage for Class 8 with Answers 36-40 | PDF
- English | Unseen Passage for Class 8 with Answers 41-45 | PDF
- English | Unseen Passage for Class 8 with Answers 46-50 | PDF
- Class 8 | English | Most Important Letter Writing 21-28 | PDF
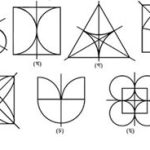
৩। নিচের চিত্রগুলোতে প্রতিসাম্য রেখা দেওয়া আছে। চিত্রগুলো সম্পন্ন করো।
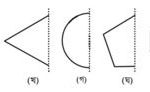
সমাধানঃচিত্রগুলো সম্পন্ন করে নিচে দেওয়া হলোঃ
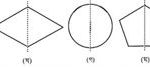
৪। নিচের চিত্রগুলোর প্রতিসাম্য রেখা অঙ্কন করো।
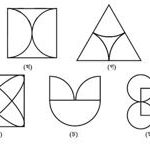
সমাধানঃচিত্রগুলোর প্রতিসাম্য-রেখা-অঙ্কন করা হলোঃ
উক্ত বিষয় সম্পর্কে কিছু জানার থাকলে কমেন্ট করতে পারেন।
আমাদের সাথে ইউটিউব চ্যানেলে যুক্ত হতে এখানে ক্লিক করুন এবং আমাদের সাথে ফেইজবুক পেইজে যুক্ত হতে এখানে ক্লিক করুন। গুরুত্বপূর্ণ আপডেট ও তথ্য পেতে আমাদের ওয়েবসাইটে ভিজিট করুন।














