৮ম শ্রেণি | গনিত | অবস্থান মানচিত্রে স্থানাঙ্ক জ্যামিতি | PDF: অষ্টম শ্রেণির প্রাথমিক গনিত বিষয়টির ৬ষ্ট অধ্যায়টি হতে বেশ কিছু গুরুত্বপূর্ণ অবস্থান মানচিত্রে স্থানাঙ্ক জ্যামিতি সম্পর্কিত সকল প্রশ্ন উত্তর গুলো আমাদের এই পোস্টে আলোচনা করা হয়েছে। অতএব সম্পূর্ণ পোস্টটি মনযোগ সহকারে পড়ুন।
অবস্থান মানচিত্রে স্থানাঙ্ক জ্যামিতি
১. একটি সরলরেখার সমীকরণ নির্ণয় করো যার ঢাল -2 এবং রেখাটি (4, -5) বিন্দু দিয়ে অতিক্রম করে।
সমাধানঃআমরা জানি,
m ঢালবিশিষ্ট (x1 , y1) বিন্দুগামী সরলরেখার সমীকরণ y – y1 = m(x – x1)
প্রদত্ত প্রশ্নে দেওয়া আছে,m = – 2 ও (x1,y1) = (4,-5)
∵ y – (-5) = -2(x – 4) [মান বসিয়ে]
বা, y + 5 = -2x + 8
বা, y = -2x + 8 – 3
বা, y = -2x + 3 [ইহাই নির্ণেয় সমীকরণ]
২. A(3, -3) ও B(4, -2) বিন্দুগামী সরলরেখার সমীকরণ নির্ণয় করো। সরলরেখাটির ঢাল কত?
সমাধানঃ
আমরা জানি,সরলরেখার ঢাল, m
= (y_1-y_2)/(x_1-x_2 )[এখানে, (x1,y1)=(3,-3); (x2,y2)=(4,-2)]
= (-3-(-2))/(3-4)
= -1/-1
= 1
আবার,m ঢালবিশিষ্ট (x1 , y1) বিন্দুগামী সরলরেখার সমীকরণ y – y1 = m(x – x1)
অর্থাৎ, y – (-3) = 1(x – 3) [A(3, -3 বিন্দুর প্রেক্ষিতে]
বা, y + 3 = x – 3
বা, y = x – 3 – 3
বা, y = x – 6
∵ A(3, -3) ও B(4, -2) বিন্দুগামী সরলরেখার সমীকরণ: y = x – 6 এবং ঢাল m = 1.
৩. দেখাও যে, A(0, -3), B(4, -2) এবং C(16, 1) বিন্দু তিনটি সমরেখ। [এটা হলো অবস্থান মানচিত্রে স্থানাঙ্ক জ্যামিতি এর ৩ নং প্রশ্ন, নিচে বিস্তারিত দেয়া আছে।]
সমাধানঃ
আমরা জানি,
m ঢালবিশিষ্ট (x1,y1) ও (x2,y2) বিন্দুগামী সরলরেখার সমীকরণঃ
y1-y2=m(x1-x2).
∵ m ঢালবিশিষ্ট A(0, -3) ও B(4, -2) বিন্দুগামী সরলরেখার সমীকরণঃ-3-(-2)=m(0-4)
বা, -3+2 = -4mবা, -1 = -4mবা, m = ¼
আবার,
m ঢালবিশিষ্ট B(4, -2) এবং C(16, 1) বিন্দুগামী সরলরেখার সমীকরণঃ
-2-1=m(4-16)
বা, -3 = m(-12)
বা, m = -3/-12
বা, m = ¼
অর্থাৎ, A(0, -3) ও B(4, -2) বিন্দুগামী সলরেখার ঢাল এবং B(4, -2) ও C(16, 1) বিন্দুগামী সলরেখার ঢাল একই।
∵ A(0, -3), B(4, -2) এবং C(16, 1) বিন্দু তিনটি সমরেখ [দেখানো হলো]।
৪. A(1, -1), B(t, 2) এবং C(t2 , t + 3) বিন্দু তিনটি সমরেখ হলে t এর সম্ভাব্য মান নির্ণয় করো।
সমাধানঃ
m ঢালবিশিষ্ট (x1,y1) ও (x2,y2) বিন্দুগামী সরলরেখার সমীকরণঃ
y1-y2=m(x1-x2)
∵ m ঢালবিশিষ্ট A(1, -1) ও B(t, 2) বিন্দুগামী সরলরেখার সমীকরণঃ
-1-2=m(1-t)
বা, -3 = m(1-t)
বা, m = -3/(1-t) ……….(i)
আবার,
m ঢালবিশিষ্ট B(t, 2) এবং C(t2, t+3) বিন্দুগামীসরলরেখারসমীকরণঃ
2-(t+3) = m(t-t2)
বা, 2-t-3 = m(t-t2)
বা, -t-1 = m(t-t2)
বা, m = (-t-1)/(t-t2) ……….(ii)
এখন, প্রদত্তবিন্দুতিনটিসমরেখ; অতএবপ্রত্যেকজোড়বিন্দুরসরলরেখারঢালএরমানসমানহবে।
∵ (i) ও (ii) হতেপাই,
-3/(1-t) = (-t-1)/(t-t2)
বা, -3(t-t2) = (1-t)(-t-1)
বা, -3t+3t2 = -(1-t)(1+t)
বা, -3t+3t2 = -(1-t2)
বা, -3t+3t2 = -1+t2
বা, -3t+3t2 +1-t2 = 0
বা, 2t2-3t+1 = 0
বা, 2t2-2t-t+1 = 0
বা, 2t(t-1)-1(t-1) = 0
বা, (2t-1)(t-1) = 0
বা, 2t-1 = 0 অথবা, t-1 = 0
বা, 2t = 1 বা, t = 1
বা, t = ½
∵ t = (1, ½)
৫. A(2, 2), B(10, 1), C(11, 9) এবং D(3, 10) এইবিন্দুগুলোলেখচিত্রেবসাওএবং AB, BC, CD, AD রেখাংশআঁকো।এইরেখাগুলোদ্বারাকীধরনেরক্ষেত্রতৈরিহয়েছে? তোমারউত্তরেরসপক্ষেযুক্তিদাও।
সমাধানঃ
লেখচিত্রে x ও y অক্ষবরাবরক্ষুদ্রতমবর্গেরবাহুরদৈর্ঘ্যকে 1 এককধরে A(2, 2), B(10, 1), C(11, 9) এবং D(3, 10) বিন্দুগুলোস্থাপনকরি। এবং AB, BC, CD, AD রেখাংশআঁকি।
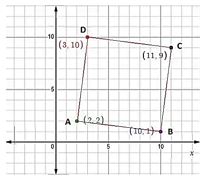
এই রেখাগুলো দ্বারা একটি বর্গক্ষেত্র তৈরি হয়েছে।
যুক্তিঃ
দুইটি বিন্দুর স্থানাংকের ভিত্তিতে,
AB= √{(10-2)2+(1-2)2}
= √{(8)2+(-1)2}
= √(64+1)
= √65
BC= √{(11-10)2+(9-1)2}
= √{(1)2+(8)2}
= √(1+64)
= √65
CD= √{(3-11)2+(10-9)2}
= √{(-8)2+(1)2}
= √(64+1)= √65
AD= √{(2-3)2+(2-10)2}
= √{(-1)2+(-8)2}
= √(1+64)
= √65
অর্থাৎ,
AB = BC = CD = AD
একইভাবে,
AC= √{(11-2)2+(9-2)2}
= √{(9)2+(7)2}
= √(81+49)
= √130
BD= √{(3-10)2+(10-1)2}
= √{(-7)2+(9)2}
= √(49+81)
= √130
অর্থাৎ, ABCD এর কর্ণদ্বয় (AC ও BD) পরস্পর সমান।
∵ AB, BC, CD, AD রেখাগুলো দ্বারা একটি বর্গক্ষেত্র তৈরি হয়েছে।

৬. তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(a, -6). যদি AB = BC হয়, তবে a এর সম্ভাব্য মানসমূহ নির্ণয় করো। a এর প্রতিটি মানের জন্য গঠিত ABC ত্রিভুজের ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
দেওয়া আছে,
তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(a, -6).
দুইটি বিন্দুর স্থানাংকের ভিত্তিতে পাই,
AB= √{(10+2)2+(6-1)2}
= √{(12)2+(5)2}
= √(144+25)
= √169
= 13
এবং,BC= √{(a-10)2+(-6-6)2}
= √{(a-10)2+(-12)2}
= √{(a-10)2+144}
প্রশ্ন অনুসারে,AB = BC
বা, 13 = √{(a-10)2+144}
বা, 169 = (a-10)2+144 [উভয়পক্ষকে বর্গ করে]
বা, (a-10)2 = 169-144
বা, (a-10)2 = 25
বা, a2-20a+102-25=0
বা, a2-20a+100-25=0
বা, a2-15a-5a+75=0
বা, a(a-15)-5(a-15)=0
বা, (a-5)(a-15)=0
বা, a-5 = 0 অথবা, a-15=0
বা, a=5 বা, a = 15
∵ a= (5,15)
এখন,
a=5 হলে, তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(5, -6);
∵ΔABC এর ক্ষেত্রফল
= ½[x1(y2-y3)+x2(y3-y1)+x3(y1-y2)] [সূত্রানুসারে]
= ½[-2(6+6)+10(-6-1)+5(1-6)]
= ½[-2×12+10(-7)+5(-5)]
= ½[-24-70-25]
= ½×(-119)
= -59.5
কিন্তু ক্ষেত্রফল ঋণাত্মক হয় না।
∵ a=5 হলে, ΔABC এর ক্ষেত্রফল 59.5 বর্গ একক।
আবার,
a=15 হলে, তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(15, -6);
∵ΔABC এর ক্ষেত্রফল
= ½[x1(y2-y3)+x2(y3-y1)+x3(y1-y2)] [সূত্রানুসারে]
= ½[-2(6+6)+10(-6-1)+15(1-6)]
= ½[-2×12+10(-7)+15(-5)]
= ½[-24-70-75]
= ½×(-169)
= -84.5
কিন্তু ক্ষেত্রফল ঋণাত্মক হয় না।
∵ a=15 হলে, ΔABC এর ক্ষেত্রফল 84.5 বর্গ একক।
পড়ুনঃ
- English | Unseen Passage for Class 8 with Answers 31-35 | PDF
- English | Unseen Passage for Class 8 with Answers 36-40 | PDF
- English | Unseen Passage for Class 8 with Answers 41-45 | PDF
- English | Unseen Passage for Class 8 with Answers 46-50 | PDF
- Class 8 | English | Most Important Letter Writing 21-28 | PDF
৭. চারটি বিন্দুর স্থানাঙ্ক A(-1, 1), B(2, -1), C(0, 3) ও D(3, 3)। বিন্দুগুলো দ্বারা গঠিত চতুর্ভুজের ক্ষেত্রফল নির্ণয় করো।
সমাধানঃ
দেওয়া আছে,
চারটি বিন্দুর স্থানাঙ্ক A(-1, 1), B(2, -1), C(0, 3) ও D(3, 3)।
বিন্দুগুলোকে গ্রাফ কাগজে বসালে নিন্মোক্ত চতুর্ভুজ ABDC পাই।
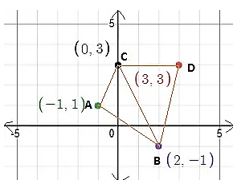
∵ ΔABC এর ক্ষেত্রফল
= ½[x1(y2-y3)+x2(y3-y1)+x3(y1-y2)] [সূত্রানুসারে]
= ½[-1(-1-3)+2(3-1)+0(1+1)]
= ½[-1×(-4)+2(2)+0(2)]
= ½[4+4+0]
= ½×(8)
= 4 বর্গ একক।
এবং,
ΔBDC এর ক্ষেত্রফল
= ½[x1(y2-y3)+x2(y3-y1)+x3(y1-y2)] [সূত্রানুসারে]
= ½[2(3-3)+3(3+1)+0(-1-3)]
= ½[2×0+3(4)+0(-4)]
= ½[0+12+0]
= ½×(12)
= 6 বর্গ একক।
∵ বিন্দুগুলো দ্বারা গঠিত চতুর্ভুজের ক্ষেত্রফল
= ΔABC এর ক্ষেত্রফল + ΔBDC এর ক্ষেত্রফল
= (4+6) বর্গ একক
= 10 বর্গ একক।
উক্ত বিষয় সম্পর্কে কিছু জানার থাকলে কমেন্ট করতে পারেন।
আমাদের সাথে ইউটিউব চ্যানেলে যুক্ত হতে এখানে ক্লিক করুন এবং আমাদের সাথে ফেইজবুক পেইজে যুক্ত হতে এখানে ক্লিক করুন। গুরুত্বপূর্ণ আপডেট ও তথ্য পেতে আমাদের ওয়েবসাইটে ভিজিট করুন।


















