৮ম শ্রেণি | গনিত | অধ্যায় ৫ম | জমির নকশায় ত্রিভুজ ও চতুর্ভুজ | PDF: অষ্টম শ্রেণির প্রাথমিক গনিত বিষয়টির ৫ম অধ্যায়টি হতে বেশ কিছু গুরুত্বপূর্ণ জমির নকশায় ত্রিভুজ ও চতুর্ভুজ সম্পর্কিত সকল প্রশ্ন উত্তর গুলো আমাদের এই পোস্টে আলোচনা করা হয়েছে। অতএব সম্পূর্ণ পোস্টটি মনযোগ সহকারে পড়ুন।
জমির নকশায় ত্রিভুজ ও চতুর্ভুজ
১। চিত্র ক-এ প্রদত্ত আকৃতি পরিমাপের ক্ষেত্রে কীভাবে সমকোণী ত্রিভুজের বৈশিষ্টট্য ব্যবহার করবে? সমস্যাটি সমাধান করো এবং পিথাগোরাসের উপপাদ্য কীভাবে সাহায্য করল যুক্তি দাও।AD = 12 cm হলে BC এর দৈর্ঘ্য নির্ণয় করো।
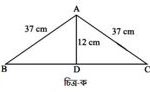
সমাধানঃ
চিত্র ক-এ প্রদত্ত আকৃতি পরিমাপের ক্ষেত্রে সমকোণী ত্রিভুজের একটি বৈশিষ্টট্য ব্যবহার করা যায়। সেটি হলোঃ-
সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান।
এখানে, দুইটি সমকোণী ত্রিভুজ ΔABD ও ΔACD আছে; তাহলে উপরোক্ত সমকোণী ত্রিভুজের বৈশিষ্ট অনুসারে আমরা লিখতে পারি-
AC2 = AD2 + DC2 …….(i)
AB2 = AD2 + BD2 ……..(ii)
এবং এই দুই সমীকরণ থেকে আমরা চিত্র ক-এ প্রদত্ত আকৃতি পরিমাপ করতে পারি।
BC এর মান নির্ণয়ঃ
(i) নং এ, AD = 12 cm; AC = 37 cm বসিয়ে পাই,
372 = 122 + DC2
বা, DC2 = 372 – 122
বা, DC2 = 1225
বা, DC = √1225 = 35
অনুরুপভাবে, (ii) নং থেকে পাই,
BD = 35
∵ BC = BD + DC = 35 + 35 = 70 cm
২। চিত্র এঁকে বা কাগজ কেটে প্রমাণ করো− বর্গের কর্ণদ্বয় পরস্পর সমান।
সমাধানঃ
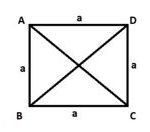
মনে করি, ABCD একটি বর্গ যাদের AC ও BD দুইটি কর্ণ। নিন্মের চিত্রে বর্গ ও তার কর্ণদ্বয়কে এঁকে দেখানো হলো। এখন এই চিত্র থেকে প্রমাণ করতে হবে যে, AC = BD.
প্রমাণঃ
ABCD বর্গে, AB = BC = CD = DA = a [∵ বর্গের চারটি বাহুর দৈর্ঘ্য সমান হয়];
আবার, ∠BCD = 90° [যেহেতু, ABCD একটি বর্গ]
∵ΔBCD হতে পিথাগোরাসের সূত্রানুসারে পাই,
BD2 = BC2 + DC2 = a2 + a2 = 2a2
বা, BD = √(2a2) = √2.a …….(i)
অনুরুপভাবে,
AC2 = CD2 + DA2 = a2 + a2 = 2a2
বা, AC = √(2a2) = √2.a …….(ii)
এখন, (i) ও (ii) হতে পাই,
AC = BD [প্রমাণিত]
৩। ধরো চারটি বাহুর দৈর্ঘ্য দেওয়া আছে 4 cm, 3 cm, 3.5 cm, 5 cm এবং যে কোনো একটি কোণ দেওয়া আছে 60 ডিগ্রি। চতুর্ভুজটি অঙ্কন করো। [জমির নকশায় ত্রিভুজ ও চতুর্ভুজ এর ৩ নং প্রশ্ন এটি; পর্যায়ক্রমে সব দেয়া হয়েছে।]
সমাধানঃ
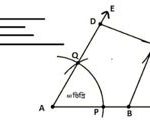
চারটি বাহুর দৈর্ঘ্য দেওয়া আছে a = 4 cm, b= 3 cm, c = 3.5 cm, d = 5 cm এবং যে কোনো একটি কোণ দেওয়া আছে 60 ডিগ্রি দেওয়া আছে। চতুর্ভুজটি অঙ্কন করতে হবে।
অঙ্কনের বিবরণঃ
(ক) যেকোনো একটি রশ্মি AF নেই এবং A কে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা AF কে P বিন্দুতে ছেদ করে।
(খ) P কে কেন্দ্র করে ঐ একই ব্যাসার্ধ নিয়ে আরও একটি বৃত্তচাপ আঁকি যা পূর্বের বৃত্তচাপকে Q বিন্দুতে ছেদ করে।
(গ) A,Q যোগ করে AE রশ্মি আঁকি। তাহলে ∠EAF = 60° অঙ্কিত হলো।
(ঘ) এখন, AF থেকে AB = a এবং AE থেকে AD = d অংশ কেটে নিই।
(ঙ) B কে কেন্দ্র করে b ও D কে কেন্দ্র করে c এর সমান ব্যাসার্ধ নিয়ে ∠DAB এর অভ্যন্তরে দুটি বৃত্তচাপ আঁকি। বৃত্তচাপদ্বয় পরস্পরকে C বিন্দুতে ছেদ করে।
(চ) D,C; B,C যোগ করি; তাহলে ABCD নির্নেয় চতুর্ভুজ অঙ্কিত হলো।
৪। চিত্র : খ-এ AB = ?
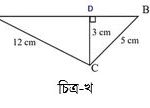
সমাধানঃ
অঙ্কনঃ
C বিন্দু থেকে AB এর উপর লম্ব AB কে যে বিন্দুতে ছেদ করে তাকে D দ্বারা চিহ্নিত করি।
AB নির্ণয়ঃচিত্রানুসারে,ΔBCD-এ,
BD2+CD2=CB2 [পিথাগোরাসের সূত্রানুসারে]
বা, BD2 = CB2-CD2
বা, BD2 = 52-32
বা, BD2 = 25 – 9
বা, BD2 = 16
বা, BD = 4 cm [বর্গমূল করে]
আবার,ΔACD-এ,
AD2+CD2=AC2 [পিথাগোরাসের সূত্রানুসারে]
বা, AD2 = AC2-CD2
বা, AD2 = 122-32
বা, AD2 = 144 – 9
বা, AD2 = 135
বা, BD = 3√15 [বর্গমূল করে]
∵ AB = AD+BD = (3√15+4) cm
৫। তোমার স্কুলের একটি দেয়াল রঙ করার জন্য যদি 15 m একটি মইকে দেয়াল থেকে 12 m দূরত্বে স্থাপন করা হয় (চিত্র:গ)। তাহলে ভূমি থেকে মইয়ের শীর্ষবিন্দু পর্যন্ত দেয়ালের উচ্চতা নির্ণয় করো।
সমাধানঃ
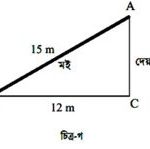
চিত্র অনুসারে,
AB = মইয়ের দৈর্ঘ্য = 15m
BC = ভুমির দৈর্ঘ্য = 12m
AC = ভূমি থেকে মইয়ের শীর্ষবিন্দু পর্যন্ত দেয়ালের উচ্চতা
এখন, AB, BC, AC মিলিত হয়ে একটি সমকোণী ত্রিভুজ উৎপন্ন করেছে যেখানে, ∠BCA = 90°।
AB2 = BC2+AC2
বা, AC2 = AB2-BC2
বা, AC2 = 152-122
বা, AC2= 225-144
বা, AC2 = 81
বা, AC = 9 [বর্গমূলকরে]
∵ভূমিথেকেমইয়েরশীর্ষবিন্দুপর্যন্তদেয়ালেরউচ্চতা 9m.
৬।চিত্র : ঘ এর আয়তক্ষেত্রটির পরিসীমা নির্ণয় করো।
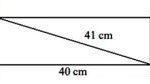
সমাধানঃ
চিত্র অনুসারে,ΔABD-এ,
BD2 = AD2+AB2
বা, AD2 = BD2-AB2
বা, AD2= 412-402
বা, AD2=1681-1600
বা, AD2 = 81
বা, AD = 9 [বর্গমূল করে]
অর্থাৎ,
আয়তক্ষেত্রটির প্রস্থ = AD = BC = 9 cm;
আয়তক্ষেত্রটির দৈর্ঘ্য = AB = CD = 40 cm.
∵ আয়তক্ষেত্রটির পরিসীমা
= 2(দৈর্ঘ্য+প্রস্থ) একক
= 2(40+9) cm= 2×49 cm= 98 cm
৭। চিত্র : ঙ এর রম্বসের কর্ণ AC = 30 cm. ও BD = 16 cm. হলে রম্বসের পরিধি নির্ণয় করো।
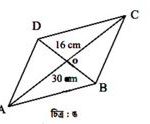
সমাধানঃ
আমরা জানি,
রম্বসের কর্ণদ্বয় নিজেদের ছেদবিন্দুতে নিজেদেরকে সমান দৈর্ঘ্যে দ্বিখন্ডিত করে এবং একে অপরের সাথে লম্বভাবে অবস্থান করে।
এখন, AC ও BD এর ছেদবিন্দু O হলে,
AO = ½×30 cm = 15 cm;
BO = ½×16 cm = 8 cm;
∵ΔABO-এ,
AB2 = AO2+OB2
বা, AB2=152+82
বা, AB2=225+64
বা, AB2=289
বা, AB = 17 [বর্গমূলকরে]
অর্থাৎ, রম্বসটিরবাহুরদৈর্ঘ্য = 17 cm
∵রম্বসটিরপরিধি = 4×17 cm = 68 cm.
৮।যদি (3, 4 ও 5) পিথাগোরিয়ানত্রয়ীহয়, তবে (3k, 4k ও 5k) পিথাগোরিয়ানত্রয়ীহবে, যেখানে k যেকোনোধনাত্মকপূর্ণসংখ্যা।উক্তিটিরযথার্থতাযাচাইকরো।
সমাধানঃ
যেহেতু (3,4 ও 5) পিথাগোরিয়ানত্রয়ীসেহেতু, 32+42=52
এখন, (3k)2+(4k)2=(5k)2 এরক্ষেত্রে k এরজন্যধণাত্মকওঋণাতমকমানধরেহিসাবকরি-
K=1 হলে,
(3.1)2+(4.1)2=(5.1)2
বা, 32+42=52
বা, 9+16=25
বা, 25=25, যাযথার্থ।
আবার,K=-1 হলে,
(3.-1)2+(4.-1)2=(5.-1)2
বা, (-3)2+(-4)2=(-5)2,
কিন্তুসমকোণীত্রিভুজেরবাহুরদৈর্ঘ্যেরমানঋণাত্মকহতেপারেনা।
আবার,K=2 হলে,
(3.2)2+(4.2)2=(5.2)2
বা, 62+82=102
বা, 36+64=100
বা, 100=100 যাযথার্থ।
আবার,K=-2 হলে,
(3.-2)2+(4.-2)2=(5.-2)2
বা, (-6)2+(-8)2=(-10)2
কিন্তুসমকোণীত্রিভুজেরবাহুরদৈর্ঘ্যেরমানঋণাত্মকহতেপারেনা।
অর্থাৎ, k এর মান ঋণাত্মক পূর্ণসংখ্যা হতে পারেনা কিন্তু সকল ধনাত্মক পূর্ণ সংখ্যা হতে পারে [উক্তিটির যথার্থতা যাচাই করা হলো]
৯।যেকোনো ত্রিভুজের দুই বাহুর মধ্য বিন্দুর সংযোগরেখা তৃতীয়বাহুর সমান্তরালও অর্ধেক।যেকোনো আকৃতির ত্রিভুজ তৈরি করে বাকাগজ কেটে পরিমাপের মাধ্যমে উক্তিটির সত্যতা নিশ্চিত করো।
সমাধানঃ
যেকোনোআকৃতিরত্রিভুজ ABC তৈরিকরিএবং AB ও AC এরমধ্যবিন্দু P ও Q সংযুক্তকরি।এখননিচেরসারণিতেবাহুরদৈর্ঘ্যপরিমাণকরেনিন্মোক্ততথ্যগুলিপূরণকরেপ্রদত্তউক্তিটিরসত্যতানিশ্চিতকরি।
বাহুর দৈর্ঘ্য বাহুর দৈর্ঘ্য অনুপাত
AP = 2.5 cm BP = 2.5 cm AP/BP = 1
AQ = 2.5 cm CE = 2.5 cm AQ/CE = 1
BC = 4 cm PQ = 2 cm BC/PQ = 2
সারণি থেকে পাই,
BP = CQ = 2.5 cm,
∵ BC || PQ
আবার,
BC/PQ = 2
বা, PQ = ½BC
অর্থাৎ, প্রদত্ত উক্তিটির সত্যতা যাচাই করা হলো।
১০। সামান্তরিকের দুইটি সন্নিহিত বাহুর দৈর্ঘ্য 6 cm ও 5 cm এবং বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 50° হলে সামান্তরিকটি অঙ্কন করো।
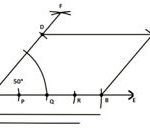
সমাধানঃ
মনে করি, একটি সামন্তরিকের দুইটি সন্নিহিত বাহুর দৈর্ঘ্য a = 6 cm ও b=5 cm এবং এই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 50°। সামন্তরিকটি আঁকতে হবে।
অঙ্কনঃ
(ক) যেকেনো রশ্মি AE লই।
(খ) A কে কেন্দ্র করে যেকোনো ব্যাসার্ধ নিয়ে একটি বৃত্তচাপ আঁকি যা AE কে P বিন্দুতে ছেদ করে। এবং অনুরুপভাবে AP এর সমান ব্যাসার্ধ নিয়ে P কে কেন্দ্র করে Q, Q কে কেন্দ্র করে R ছেদ বিন্দু লই।
(গ) Q ও R কে কেন্দ করে AE এর একই দিকে AR এর সমান ব্যাসার্ধ নিয়ে দুইটি বৃত্তচাপ আঁকি যারা পরস্পরকে F বিন্দুতে ছেদ করে। তাহলে, ∠EAF = 50° অঙ্কিত হলো।
(ঘ) A, F যোগ করি।
(ঙ) AE থেকে AB = a, AF থেকে AD = b কেটে নিই।
(চ) D কে কেন্দ্র করে a এর সমান ব্যাসার্ধ ও B কে কেন্দ্র করে b এর সমান ব্য্যাসার্ধ নিয়্যে ∠DAB এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি যারা পরস্পরকে C বিন্দুতে ছেদ করে।
(ছ) D,C ও A,B যোগ করি। তাহলে, ABCD-ই নির্ণেয় সামন্তরিক।

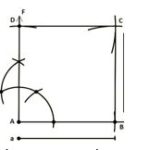
১১। একটি বর্গের এক বাহুর দৈর্ঘ্য 5 cm হলে বর্গটি অঙ্কন করো।
সমাধানঃ
মনে করি একটি বর্গের এক বাহুর দৈর্ঘ্য a = 5 cm দেওয়া আছে, বর্গটি আঁকতে হবে।
অংকনঃ
(ক) যেকোনো রশ্মি AE নিই।
(খ) AE থেকে AB = a কেটে নিই।
(গ) A বিন্দুতে AF লম্ব আঁকি এবং AF থেকে AD=a কেটে নিই।
(ঘ) B ও D কে কেন্দ্র করে a এর সমান ব্যাসার্ধ নিয়ে ∠DAB এর অভ্যন্তরে দুইটি বৃত্তচাপ আঁকি যারা পরস্পরকে C বিন্দুতে ছেদ করে।
(ঙ) D,C ও B,C যোগ করি। তাহলে ABCD-ই নির্ণেয় বর্গ।
১২. একটি সামান্তরিক আকৃতির জমির দুটি সন্নিহিত বাহুর দৈর্ঘ্য 4 m ও 5 m এবং একটি কর্ণের দৈর্ঘ্য 7 m। সামান্তরিকটির ক্ষেত্রফল নির্ণয় করো।
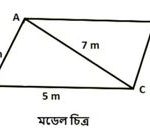
সমাধানঃ
প্রদত্ত গাণিতিক প্রশ্ন অনুসারে নিন্মোক্ত মডেল চিত্রটি অঙ্কন করি-
চিত্র অনুসারে,
ΔABC-এ
পরিসীমা = (4+5+7) m = 16 m;
∵ অর্ধ-পরিসীমা, s = 16/2 m = 8 m;
এবং, তিনটি বাহু a,b, c এর মান যথাক্রমে 4m, 5m, 7m;
∵ΔABC-এর ক্ষেত্রফল
= √{s(s-a)(s-b)(s-c)} বর্গ একক
= √{8(8-4)(8-5)(8-7)} m2
= √(8×4×3×1) m2
= √96 m2
এখন, সামন্তরিকের যেকোনো কর্ণ সামন্তরিকটিকে দুইটি সমান ত্রিভুজ ক্ষেত্রে বিভক্ত করে।
∵ সামন্তরিকটির ক্ষেত্রফল = 2×√96 m2 = 19.5959 m2 (প্রায়)
১৩। ABCD আয়তাকার জমির AB = 10 m এবং কর্ণ AC = 16 m। কর্ণদ্বয়ের ছেদবিন্দু G হলে ∆AGB এর ক্ষেত্রফল নির্ণয় করো।
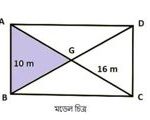
সমাধানঃ
প্রদত্ত প্রশ্নের একটি গাণিতিক মডেল চিত্র অঙ্কন করি যা নিন্মরুপঃ
চিত্র বা শর্ত অনুসারে,আয়তাকার জমির কর্ণ =AC =BD =16m [যেহেতু আয়তক্ষেত্রের কর্ণদ্বয় সমান];
এবং AG = BG = 16/2 m = 8 m [যেহেতু আয়তক্ষেত্রের কর্ণদ্বয় একে আপরকে সমদ্বিখন্ডিত করে];
∵∆AGB-এর ক্ষেত্রে,
তিনটি বাহু a, b, c এর দৈর্ঘ্য = 10m, 8m, 8m;
পরিসীমা = (10+8+8) m = 26 m;
∵ অর্ধ-পরিসীমা, s = 26/2 m = 13 m;
∵∆AGB-এর ক্ষেত্রফল
= √{s(s-a)(s-b)(s-c)} বর্গ একক
= √{13(13-10)(13-8)(13-8)} m2
= √(13×3×5×5) m2
= √975 m2
= 31.22499 m2
পড়ুনঃ
- English | Unseen Passage for Class 8 with Answers 31-35 | PDF
- English | Unseen Passage for Class 8 with Answers 36-40 | PDF
- English | Unseen Passage for Class 8 with Answers 41-45 | PDF
- English | Unseen Passage for Class 8 with Answers 46-50 | PDF
- Class 8 | English | Most Important Letter Writing 21-28 | PDF
১৪। প্রদত্ত আকৃতিগুলোর ক্ষেত্রফল পরিমাপ করো:
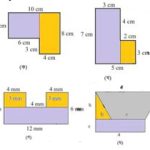
সমাধানঃ
(ক)
ক-আকৃতিকে আমরা দুইটি অংশে বিভক্ত করি-
তাহলে,
ক-আকৃতির ক্ষেত্রফল
= ১ম আয়তের ক্ষেত্রফল + ২য় আয়তের ক্ষেত্রফল
= 6cm×5cm + 8cm×4cm
= 30cm2 + 32cm2
= 62cm2
(খ)খ-আকৃতিকে আমরা দুইটি অংশে বিভক্ত করি-
তাহলে,
খ-আকৃতির ক্ষেত্রফল
= ১ম আয়তের ক্ষেত্রফল + ২য় আয়তের ক্ষেত্রফল
= 7cm×3cm + 2cm×3cm
= 21cm2 + 6cm2
= 27cm2
(গ)গ-আকৃতিকে আমরা তিনটি অংশে বিভক্ত করি-
তাহলে,
গ-আকৃতির ক্ষেত্রফল
=১ম আয়তের ক্ষেত্রফল+২য় আয়তের ক্ষেত্রফল+৩য় আয়তের ক্ষেত্রফল
= 4cm×3cm + 4cm×3cm + 12cm×3cm
= 12cm2 + 12cm2 + 36cm2
= 60cm2
(ঘ)ঘ-আকৃতিকে আমরা তিনটি অংশে বিভক্ত করি-
তাহলে,
ঘ-আকৃতির ক্ষেত্রফল
= ১ম ত্রিভূজের ক্ষেত্রফল + ২য় ট্রপিজিয়ামের ক্ষেত্রফল
+ ৩য় আয়তের ক্ষেত্রফল
= ½×b×h + ½(d+e)h + a×c
= ½bh + ½dh+½eh + ac
= ½h(b+d+e)+ac
উক্ত বিষয় সম্পর্কে কিছু জানার থাকলে কমেন্ট করতে পারেন।
আমাদের সাথে ইউটিউব চ্যানেলে যুক্ত হতে এখানে ক্লিক করুন এবং আমাদের সাথে ফেইজবুক পেইজে যুক্ত হতে এখানে ক্লিক করুন। গুরুত্বপূর্ণ আপডেট ও তথ্য পেতে আমাদের ওয়েবসাইটে ভিজিট করুন।

















